| Главная » Статьи » Программирование |
Нахождение НОД(наибольшего общего делителя) в c++
Даны два целых неотрицательных числа и . Требуется найти их наибольший общий делитель, т.е. наибольшее число, которое является делителем одновременно и , и . На английском языке "наибольший общий делитель" пишется "greatest common divisor", и распространённым его обозначением является : 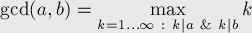 (здесь символом "" обозначена делимость, т.е. "" обозначает " делит ") Когда оно из чисел равно нулю, а другое отлично от нуля, их наибольшим общим делителем, согласно определению, будет это второе число. Когда оба числа равны нулю, результат не определён (подойдёт любое бесконечно большое число), мы положим в этом случае наибольший общий делитель равным нулю. Поэтому можно говорить о таком правиле: если одно из чисел равно нулю, то их наибольший общий делитель равен второму числу. Алгоритм Евклида, рассмотренный ниже, решает задачу нахождения наибольшего общего делителя двух чисел и за . Данный алгоритм был впервые описан в книге Евклида "Начала" (около 300 г. до н.э.), хотя, вполне возможно, этот алгоритм имеет более раннее происхождение. Реализация: int gcd (int a, int b) { if (b == 0) return a; else return gcd (b, a % b); } Еще один вариант(некурсивный): int gcd (int a, int b) { while (b) { a %= b; swap (a, b); } return a; } Источник: http://e-maxx.ru/upload/e-maxx_algo.pdf | |
| Просмотров: 15535 | Теги: | Рейтинг: 4.5/2 |
| Всего комментариев: 0 | |